About Evolutionary Action

Let genotype (γ) be the sequence space (Smith 1970) and phenotype (φ) be the fitness landscape (Wright 1932). Then, each species reaches an optimum in fitness (equilibrium position) that corresponds to their reference genome. Polymorphisms correspond to small displacements away from the equilibrium position and they may accumulate, while deleterious mutations are big steps and they are selected against. Our hypothesis is that γ and φ are coupled to each other by a continuous and differentiable function f, and this function also holds across species. Then, a small genotype perturbation dγ will change the fitness phenotype by dφ, which will be given by:

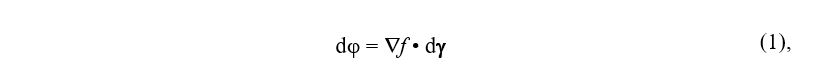
where ∇f is the gradient of f and • denotes the scalar product. Neglecting the higher order (epistatic) terms, a single amino acid change at sequence position i, from X to Y, will drive a phenotype change Δφ that equals:

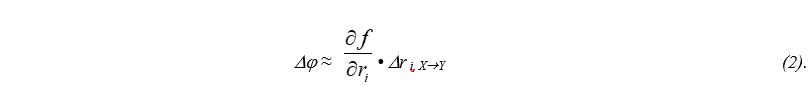
This action equation states that the fitness effect of a single mutation is proportional to the sensitivity of the phenotype to changes at the position i and the magnitude of the genotype change. Although the function f is unknown, the terms of expression (2) can be approximated from empirical data on protein evolution.

We approximated the gradient δf/δri with Evolutionary Trace (ET) scores (Lichtarge et al. 1996; Mihalek et al. 2004; Lichtarge and Wilkins 2010), because they represent the phylogenetic distance (~Δf) that corresponds to a mutation at each residue i (Δri=1). To measure the magnitude of a substitution (Δri,X->Y), we used substitution odds (Henikoff and Henikoff 1992; Overington et al. 1992) calculated for strata of ET scores and structural features (Overington et al. 1992).